
Pressione specifica della neve sulle strutture di sostegno del manto nevoso nella zona di distacco delle valanghe
La determinazione delle azioni esercitate dalla pressione della neve sulle strutture di sostegno permanenti del manto nevoso nella zona di distacco delle valanghe risulta essere un operazione assai complessa. Spesso infatti si manifestano fenomeni difficilmente prevedibili anche con attente osservazioni e misurazioni. Il manto nevoso reale è un mezzo stratificato, disomogeneo, anisotropo dove la densità e le velocità di scorrimento e di slittamento, che determinano l’entità degli sforzi di taglio e quindi la pressione, variano da strato a strato e da zona a zona; inoltre il manto nevoso modifica le proprie caratteristiche meccaniche più o meno rapidamente nel tempo e nello spazio, in funzione della temperatura.
Per il calcolo delle forze agenti sulla struttura si fa generalmente riferimento alle Direttive Svizzere per la “Costruzione di opere di premunizione contro le valanghe nella zona di distacco” edizione 2007 emanate dall’ UFAM (Ufficio Federale per l’Ambiente) e dal WSL (Istituto Federale Svizzero per lo Studio della Neve e delle Valanghe).
L’adottare come riferimento per il calcolo delle forze agenti sulla struttura le Direttive Svizzere, la cui validità è riconosciuta a livello internazionale e supportata da più di cinquant’anni di esperienza e di validazione sul campo di opere realizzate e calcolate in base alle stesse, non esonera il progettista dell’intervento da una indispensabile verifica della loro applicabilità, e, se il caso, da una opportuna ed attenta taratura dei parametri, particolarmente per contesti geografici e climatici differenti da quello alpino svizzero. E’ evidente infatti che la neve degli Appennini, dei Pirenei o quella del Caucaso, dell’Islanda o della costa occidentale degli Stati Uniti presenta caratteristiche assai diverse dalla neve alpina e il non tenerne debito conto può comportare spiacevoli sorprese, fino al collasso delle strutture.
Scopo delle opere di sostegno è quello di impedire il distacco di valanghe o, per lo meno, di rendere inoffensivi i movimenti di neve, che non possono essere completamente arrestati, al loro sorgere in modo tale da non acquistare velocità e quindi energia distruttiva. Le valanghe in pieno movimento esercitano forze che le opere di sostegno, di regola, non sono in grado di sopportare.
Le opere di sostegno devono opporre allo scorrimento ed eventualmente allo slittamento del manto nevoso una superficie di sostegno ancorata al terreno, più o meno perpendicolare al pendio e con un’altezza almeno pari a quella del manto nevoso con un tempo di ritorno 100 anni. Ciò comporta un’azione di sbarramento, e le velocità di scorrimento e di slittamento si riducono man mano che la neve si avvicina all’ostacolo.
Secondo le Direttive svizzere la pressione specifica esercitata dalla neve su di un’opera di stabilizzazione del manto nevoso dipende dai seguenti fattori locali:
- ρ = densità della neve, dipende dal tipo di neve.
- Hestr = altezza estrema della neve sul posto dell’opera misurata verticalmente (valore più elevato dell’altezza massima della neve misurata in posto durante un lungo periodo di anni o prevista con metodi di analisi statistica).
- k = fattore di scorrimento, dipendente dalla densità della neve e dalla acclività del terreno.
- N = coefficiente di slittamento, dipendente dal tipo di vegetazione, dalla rugosità del terreno e dalla sua esposizione al sole.
- fc = fattore di altitudine, che caratterizza la dipendenza della densità della neve dall’altitudine.
- fr = fattore marginale, dipendente dagli intervalli laterali tra le opere e dal coefficiente di slittamento.
- fs = fattore di riduzione per tener conto di una superficie di appoggio flessibile da adottare nel caso di reti da neve.
- Hk = altezza tra il bordo superiore della rete ed il suolo, misurata verticalmente.
- Dk = distanza tra il bordo superiore della rete ed il suolo, misurata perpendicolarmente al pendio (spessore della neve).
- ψ = angolo massimo di inclinazione del pendio nella zona di distacco.
Alcuni di questi fattori vengono determinati sul posto, mentre altri si ottengono da relazioni generali.
Nella sua formulazione più generale, riportata nelle Direttive svizzere, la componente parallela al pendio della pressione specifica (per metro lineare) della neve, S’N, su una superficie perpendicolare al pendio e di lunghezza illimitata lungo la linea di livello è data dalla seguente formula:
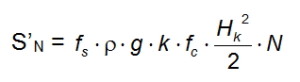 [1]
[1]
La pressione specifica della neve S’N fornita dalla [1] è generalmente considerata come costante ed uniformemente distribuita sull’altezza dell’opera di sostegno. Si tratta di una semplificazione drastica in quanto la distribuzione della pressione all’interno del manto nevoso è assai complessa anche in presenza di una coltre nevosa omogenea.
La formula [1] deriva da una semplificazione delle equazioni differenziali del manto nevoso (componente statica e componente dinamica) considerato come mezzo continuo assimilabile ad un fluido viscoso di tipo newtoniano incomprimibile con comportamento lineare. La realtà è molto più complessa ed in letteratura esistono trattazioni di tipo numerico più sofisticate che partono da modelli costitutivi non lineari decisamente più accurati, che consentono, tra l’altro, di conoscere la reale distribuzione delle pressioni della neve sulla struttura ed ai quali è opportuno far riferimento per lo studio di casi particolarmente complessi.
Dalla formula [1] si evince che per il calcolo della pressione specifica della neve su di una struttura fermaneve risulta essere determinante, e quindi dimensionante, il valore dello spessore del manto nevoso Dk.
La componente perpendicolare al pendio della pressione specifica (per metro lineare) della neve S’Q su una superficie di sostegno perpendicolare al pendio si manifesta quando, a contatto della stessa, viene impedito l’assestamento (aderenza, rugosità) ed è funzione di S’N secondo la formula:
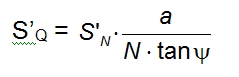 [2]
[2]
Dove a è una costante che può variare tra 0,30 ≤ a ≤ 0,50, assumendo i valori più bassi per neve densa e i valori più alti per neve a debole coesione.
E’ interessante vedere come variano i valori S’N ed S’Q in funzione del variare dei termini r (m), N, ψ e Dk, assumendo a = 0,50 , fc ed fs costanti.
Le formule [1] e [2] sono state dunque graficate, assumendo valori costanti per fs = 0,8 (corrispondente al caso tipico delle reti da neve, che risulta essere la tipologia di struttura fermaneve maggiormente impiegata sull’arco alpino) e per fc = 1,1 (corrispondente al caso tipico di quota della zona di distacco pari a 2000 m s.l.m. in accordo alle Direttive svizzere) e facendo variare singolarmente i seguenti parametri:
- densità media del manto nevoso nella zona di distacco ρ (t/m3)
- spessore del manto nevoso nella zona di distacco Dk (m)
- angolo di inclinazione del pendio nella zona di distacco ψ (°)
- coefficiente di slittamento nella zona di distacco N
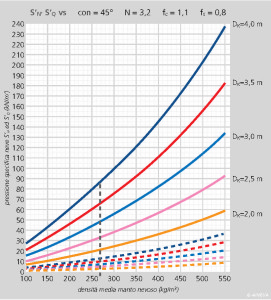
FIGURA 2 – Variazione del valore delle componenti S’N ed S’Q della pressione specifica della neve sull’opera di sostegno in funzione del valore della densità media del manto nevoso r per diversi valori di spessore del manto nevoso Dk, nel caso in cui ψ = 45° ed N = 3,2.
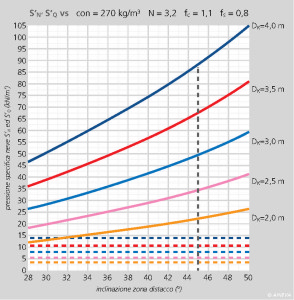
FIGURA 3 – Variazione del valore delle componenti S’N ed S’Q della pressione specifica della neve sull’opera di sostegno in funzione del valore dell’inclinazione del pendio nella zona di distacco y per diversi valori di spessore del manto nevoso Dk, nel caso in cui ρ = 270 kg/m3 ed N = 3,2.
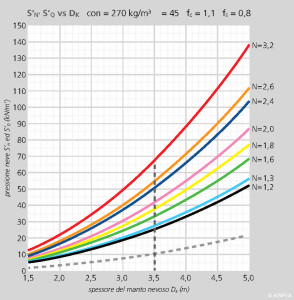
FIGURA 4 – Variazione del valore delle componenti S’N ed S’Q della pressione specifica della neve sull’opera di sostegno in funzione del valore dello spessore del manto nevoso Dk, per diversi valori del coefficiente di slittamento N, nel caso in cui ρ = 270 kg/m3 e Ψ = 45°.
Nei grafici l’andamento della componente S’N è indicato dalla linea continua, mentre l’andamento di S’Q è indicato dalla linea tratteggiata.
La figura 2 evidenzia che il valore della componente parallela al pendio della pressione specifica della neve, S’N, nell’intervallo 100 kg/m3 (neve fresca farinosa) ≤ ρ ≤ 550 kg/m3 (neve molto umida), cresce con andamento curvilineo di forma approssimativamente parabolica al crescere del valore della densità media ρ. All’aumentare della densità Ρ, per i diversi valori di spessore del manto nevoso Dk, le parabole tendono a divergere. Ciò sta a significare, che la pressione specifica della neve non è direttamente proporzionale alla densità media del manto nevoso e che un aumento della densità media si riflette in un maggiore aumento della pressione specifica della neve. Passando da un valore di densità media di 270 kg/m3 (valore standard conforme alle Direttive svizzere per le Alpi svizzere) ad uno di 450 kg/m3, a fronte di un corrispondente incremento del 66,67% del valore della densità media, si ha un incremento del 95,60% del valore di S’N: in pratica, quasi un raddoppio della forza agente sull’opera di sostegno!
Anche il valore della componente perpendicolare al pendio della pressione specifica della neve, S’Q, segue lo stesso andamento approssimativamente parabolico assumendo però valori corrispondenti che risultano essere 6,4 volte inferiori di quelli di S’N.
La figura 3 evidenzia che il valore della componente parallela al pendio della pressione specifica della neve, S’N, nell’intervallo 28° ≤ ψ ≤ 50°, cresce con andamento curvilineo di forma parabolica al crescere del valore dell’inclinazione y della zona di distacco, mentre il valore della componente normale al pendio della pressione specifica della neve, S’Q, rimane costante, cioè risulta essere del tutto indipendente dal valore di ψ.
Poiché, nella maggior parte dei casi, l’inclinazione della zona di distacco delle valanghe, almeno per quanto concerne la neve di tipo alpino, è compresa tra i 30° e i 50°, si può notare come passando da 30° a 50° di inclinazione della zona di distacco si ha un raddoppio del valore della componente parallela al pendio della pressione specifica della neve S’N.
La figura 4 evidenzia che il valore della componente parallela al pendio della pressione specifica della neve, S’N, nell’intervallo 1,5 m ≤ Dk ≤ 5,0 m, cresce con andamento curvilineo di forma parabolica al crescere del valore dello spessore del manto nevoso Dk nella zona di distacco, mentre il valore della componente normale al pendio della pressione specifica della neve, S’Q, cresce anch’esso in modo parabolico, ma risulta essere del tutto indipendente dal valore di N. All’aumentare dello spessore Dk, per i diversi valori del coefficiente di slittamento N, le parabole tendono a divergere. Passando da un terreno di classe 3 con esposizione al sole, caratterizzato da N = 2,4 ad un terreno di classe 4 con esposizione al sole, caratterizzato da N = 3,2, si ha un incremento del valore di S’N pari al 33% mentre S’Q rimane costante. Si vuole inoltre richiamare l’attenzione sul fatto che passando da un valore di Dk = 3,0 m ad uno di Dk = 4,0 m, a fronte di un incremento del 33% del valore di Dk si ha un incremento del 78% del valore di S’N e di S’Q; vale a dire un corrispondente incremento di S’N e S’Q pari a più del doppio. Ciò comporta un notevole aumento delle forze agenti sulla struttura di sostegno del manto nevoso e quindi, in definitiva, delle forze agenti sulle fondazioni. Per questo motivo, oltre un certo valore di Dk (max 4,5 m), le strutture di sostegno del manto nevoso diventano decisamente antieconomiche o quantomeno estremamente complesse da fondare su terreni di scadenti caratteristiche meccaniche.
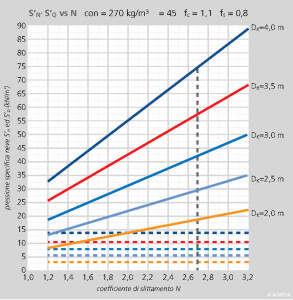
La figura 5 evidenzia che il valore della componente parallela al pendio della pressione specifica della neve, S’N, nell’intervallo 1,2 ≤ N ≤ 3,2 m, cresce con andamento rettilineo (con retta avente pendenza crescente al crescere del valore Dk) al crescere del valore del coefficiente di slittamento N: S’N è direttamente proporzionale ad N; mentre il valore della componente normale al pendio della pressione specifica della neve, S’Q, rimane costante e pertanto risulta essere del tutto indipendente dal valore di N.
Poiché il valore del coefficiente di slittamento N, per la neve alpina, varia tra 1,2 (pendii non esposti al sole, con rugosità elevata) e 3,2 (pendii esposti al sole con rugosità molto bassa), passando dal valore minimo N=1,2 al valore massimo N=3,2 si ha un incremento della pressione specifica della neve S’N pari a ca. 2,7 volte.
I grafici riportati possono costituire un rapido ed utile strumento per un calcolo preliminare di massima delle pressioni specifiche agenti sulle reti da neve e, moltiplicando i valori della pressione specifica per 1,25, delle pressioni specifiche agenti sui ponti e sulle rastrelliere da neve.
Per vedere l’articolo pubblicato sulla rivista Neve e Valanghe n. 75 clicca qui
- Posted by studiocastaldini
- On 16/05/2016





0 Comments